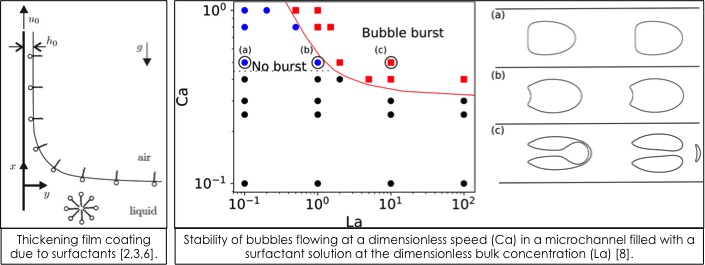
Although the concepts of surface viscosity and elasticity date back to the Belgian scientist Plateau in the 19th century, they have only later been formalized mathematically and subsequently been used in quantitative descriptions of surface flows. The concepts of surface viscosity and elasticity (Marangoni) effects are intimately related, and are not always distinguishable in an experimental setting. One such setting is the drainage of lamella in foams that we first investigated [1]. Another setting is the Landau-Levich-Derjaguin dip-coating flow, wherein a film of liquid is ‘deposited’ onto a solid substrate as it is withdrawn from a bath. This process is so fundamental to coating flows that it is ubiquitous in today’s coating technology. It is commonly assumed that, as for pure liquids, there is no thickening for liquids containing large amounts of soluble surfactants, i.e. the substrate withdrawal does not induce Marangoni stresses. However, in some cases thickening does occur, as demonstrated experimentally by collaborators at LPS, Orsay [3]. On the theoretical front, we have shown that thickening in the absence of Marangoni effects can be rationalized by surface viscosity [2], while surface (Marangoni) elasticity can be quantified by a surface rigidity parameter that is not an intrinsic parameter of the interface but depends on the film dynamics [6,7]. The transition from stress-free to rigid interface by increasing the concentration of soluble surfactants has also been explored with deformable bubbles flowing in microchannels [8].
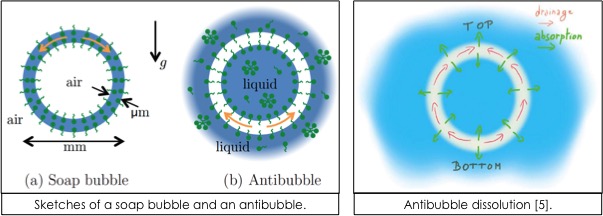
An antibubble is an intriguing object, which owns its name for being the contrary of a soap bubble. If a soap bubble is a thin spherical shell of soapy liquid surrounded by air, an antibubble is a thin spherical shell of air surrounded by liquid. We have rationalised the minute-wise lifetime of antibubbles using the concept of surface rheology [4]. We then showed that the gas content in the surrounding liquid has a crucial importance [5] and can explain most of the dispersion of antibubble lifetimes previously reported in literature [9]. In order to investigate the antibubble dynamics in a more systematic way, we have developed an on-demand antibubble generator, for which a patent application has been filed.
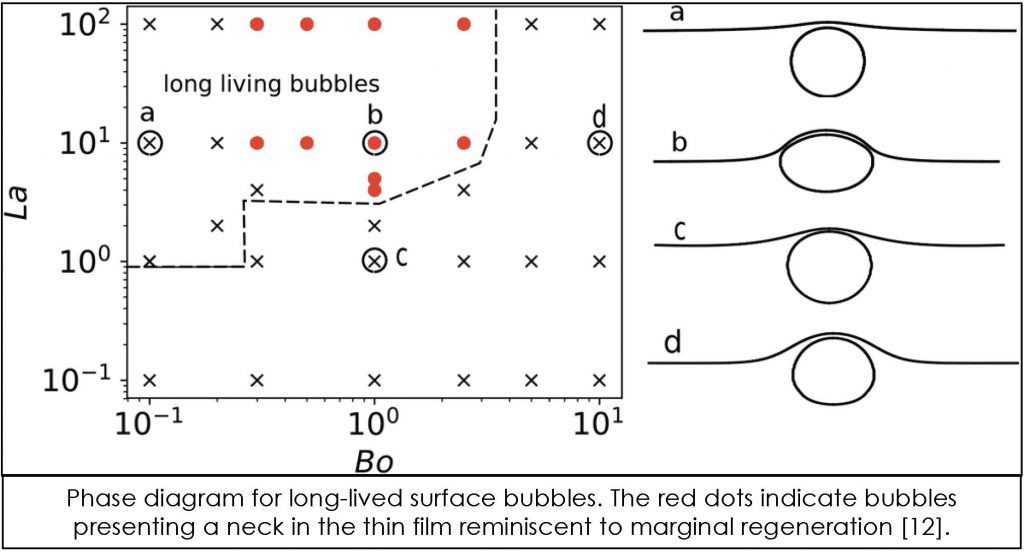
We have also investigated the influence of insoluble surfactants and the concomitant Marangoni elasticity on the Rayleigh-Plateau instability, focusing on the conditions leading to the formation of satellite droplets [10], often undesirable in applications. The influence of soluble surfactants has also been studied in the context of surface bubbles, taking into account the surface history during the rising phase [12]. Amazingly, this studied allowed to rationalise an ancestral method for determining the amount of alcohol in mezcal by considering the lifetime of surface bubbles [11].
[12] Atasi O., Legendre D., Haut B., Zenit R. & Scheid B., Lifetime of surface bubbles in surfactant solutions, Langmuir 36, 7749-7764 (2020)
[11] Rage G., Atasi O., Wilhelmus M.M., Hernandez-Sanchez J.F., Haut B., Scheid B., Legendre D. & Zenit R., Bubbles determine the amount of alcohol in Mezcal, Scientific Reports 19, 11014 (2020)
[10] Martinez-Calvo A., Rivero-Rodriguez J., Scheid B. & Sevilla A., Natural break-up and satellite formation regimes of surfactant-laden liquid threads, Journal of Fluid Mechanics 883, A35 (2020)
[9] Vitry Y., Dorbolo S., Vermant J. & Scheid B., Controlling the lifetime of antibubbles, Advances in Colloid and Interface Science 270, 73 (2019)
[8] Atasi O., Haut B., Pedrono A., Scheid B. & Legendre D., Influence of Soluble Surfactants and Deformation on the Dynamics of Centered Bubbles in Cylindrical Microchannels, Langmuir 34, 10048-10062 (2018)
[7] Champougny L., Rio E., Restagno F. & Scheid B., The break-up of free films pulled out of a pure liquid bath, Journal of Fluid Mechanics 811, 499-524 (2017)
[6] Champougny L., Scheid B., Restagno F., Vermant J. & Rio E., Surfactant-induced rigidity of interfaces: a unified approach to free and dip-coated films, Soft Matter 11, 2758 (2015)
[5] Scheid B., Zawala J. & Dorbolo S., Gas dissolution in antibubble dynamics, Soft Matter 10, 7096 (2014)
[4] Scheid B., Dorbolo S., Arriaga L.R. & Rio E., Antibubbles dynamics: the drainage of an air film with viscous interfaces, Physical Review Letters 109, 264502 (2012)
[3] Delacotte J., Montel L., Restagno F., Scheid B., Dollet B., Stone H.A., Langevin D. & Rio E., Plate coating: influence of concentrated surfactants on the thickening, Langmuir 28, 3821 (2012)
[2] Scheid B., Delacotte J., Dollet B., Rio E., Restagno F., van Nierop E. A., Cantat I., Langevin D. & Stone H. A., The role of surface rheology in liquid film formation, Europhysics Letters 90, 24002 (2010)
[1] van Nierop E., Scheid B. & Stone H.A., On the thickness of soap films: An alternative to Frankel’s law, Journal of Fluid Mechanics 602, 119-127 (2008) Corrigendum: Journal of Fluid Mechanics 630, 443-444 (2009)