Use the software WaveMaker for falling film simulations [24]
Falling liquid films have been the subject of many fundamental research efforts. The complexity of this fluid dynamics problem includes many challenging aspects such as the ultimate goal of predicting heat and mass transfer efficiencies in presence of three-dimensional patterns arising due to one or several instabilities including Kapitza, Rayleigh-Plateau, Rayleigh-Taylor or Marangoni instability, or a combination of those. Due to their wide range of applications, such as in sea water desalinisation, milk or orange juice concentration, sugar production, liquid air distillation, etc., liquid falling films are still currently the subjects of active research. On the fundamental front, a falling liquid film can serve as a canonical system to study spatio-temporal chaos and weak/dissipative turbulence. Indeed, hydrodynamic waves arising at the surface of a falling film exhibit several spatio-temporal transitions from 2D traveling waves to 3D wave patterns, leading to solitary pulses and eventually interfacial turbulence [9].
In falling liquid films, the waves are typically long as compared to the film thickness, deformations of the free surface are weak and the viscosity of the fluid ensures a great coherence of the flow across the film. These two peculiarities enable to drastically reduce the complexity of the basic equations and to obtain model systems of reduced dimensionality. Developing such models in various configurations has been one of the main research topics of the PhD.
Long-wave asymptotic equation for the evolution of the film thickness is only valid for small flow rate (or Reynolds number), as we have shown [6] where we systematically analyzed the validity domain of such equation, including thermocapillary (Marangoni) effect. The integral boundary layer approach leads in turn to a system of coupled equations for the film thickness, the flow rate and the interfacial temperature. Though valid for larger flow rates, integral boundary layer equations do not correctly predict the threshold for the primary instability leading to hydrodynamic waves. We have thus applied a weighted residual method leading to a model valid in a wider range of Reynolds number than previous models in literature, and including thermocapillary effect [7,8,11].
Based on the same techniques, we have also extended the model to three-dimensions and have obtained, for isothermal conditions, excellent agreements with various and independent experimental data on 3D secondary hydrodynamic instability and resulting wave patterns [9,14]. For non-isothermal conditions, our theory predicts intricate interactions between hydrodynamic waves and thermocapillary effect [12], which can lead for specific parameters to the spontaneous channelling of 2D solitary pulses [13]. Such regime is predicted to enhance heat transfer properties and experimental verifications have been recently obtained [16].
Since the thermocapillary effect modifies the wave pattern in falling films, which can affect the heat transfer properties but also generate undesirable dry patches, we also explored the control of deformations by imposing a non-homogeneous heating at the wall [2,4]. Furthermore, a local temperature gradient imposed at the wall and aligned with the flow can generate a liquid bump as in the “tears of wine” problem, which can become unstable and breaks into rivulet-like pattern [1,3]. We studied this instability experimentally and proposed a mechanism for its onset [5]. Most of our works related to the dynamics of falling liquid films, including wave pattern formation and heat transfer, have been reported in a monograph. A phase diagram for the onset of rolling waves and flow reversal in inclined falling films has also been proposed [15] and the numerical code for simulating falling liquid film is now available in open source [24].
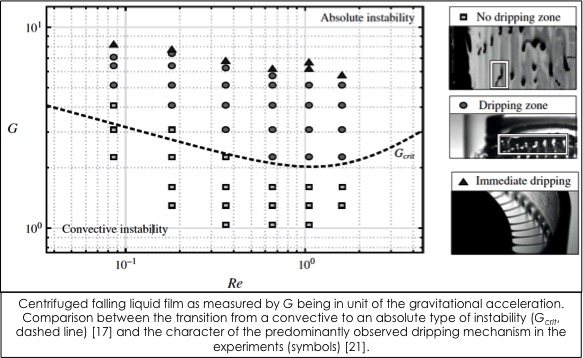
A recent extension of this research topic is to study the coupling between Kapitza waves and Rayleigh-Taylor instability when a film is suspended under an inclined plate [17,18,25]. Such a coupling can lead to intricate 3D rivulet patterns, which might be at the origin of speleothem morphogenesis [27], or which might be promising in terms of enhancing heat and mass transfer in industrial processes [20]. It is however of crucial importance to prevent the dripping phenomenon, the onset of which has been investigated in a suspended film along a plate [23] or a curved surface [22]. Comparable destabilising body forces have also been explored in centrifuged falling films [21], as well as in dielectric falling films submitted to an electric field [26]
[27] Ledda P.G., Balestra G., Lerisson G., Scheid B., Wyart M. & Gallaire F., Hydrodynamic-driven speleothem morphogenesis: a monogenic signal based study of the impulse response, Journal of Fluid Mechanics 910, A53 (2021)
[26] Rohlfs W., Cammiade L. M. F., Rietz M. & Scheid B., On the effect of electrostatic surface forces on dielectric falling films, Journal of Fluid Mechanics 906, A18 (2021)
[25] Charogiannis A., Denner F., van Wachem B.G.M., Kalliadasis S., Scheid B. & Markides C.N., Experimental investigations of liquid falling films flowing under an inclined planar substrate, Physical Review Fluids 3, 114002 (2018)
[24] Rohlfs W., Rietz E. & Scheid B., WaveMaker: The three-dimensional wave simulation tool for falling liquid films, SoftwareX 7, 211-216 (2018)
[23] Kofman N., Rohlfs W., Gallaire F., Scheid B. & Ruyer-Quil C., Prediction of two-dimensional dripping onset of a liquid film under an inclined plane, International Journal of Multiphase Flow 104, 286-293 (2018)
[22] Balestra G., Kofman N., Brun P.-T., Scheid B. & Gallaire F., Three-dimensional Rayleigh-Taylor instability under a unidirectional curved substrate, Journal of Fluid Mechanics 837, 19-47 (2018)
[21] Rietz M., Scheid B., Gallaire F., Kofman N., Kneer R. & Rohlfs W., Dynamics of falling films on the outside of a vertical rotating cylinder: waves, rivulets and dripping transitions, Journal of Fluid Mechanics 832, 189-211 (2017)
[20] Wylock C. & Scheid B., Two-dimensional modelling of an absorbing falling film in its development zone, AIChE Journal 63, 4370 (2017)
[19] Mendez M.A., Scheid B. & J.-M. Buchlin, Low Kapitza Falling Liquid Films, Chemical Engineering Science 170, 122 (2017)
[18] Rohlfs W., Pischke P. & Scheid B., Hydrodynamics waves in films flowing under an inclined plane, Physical Review Fluids 2, 044003 (2017)
[17] Scheid B., Kofman N. & Rohlfs W., Critical inclination for Absolute/Convective instability transition in inverted falling films, Physics of Fluids 28, 044107 (2016)
[16] Rietz M., Rohlfs W., Kneer R. & Scheid B., Experimental investigation of thermal structures in regular three-dimensional falling films, European Physical Journal Special Topics 224, 355 (2015)
[15] Rohlfs W. & Scheid B., Phase diagram for the onset of rolling waves and flow reversal in inclined falling films, Journal of Fluid Mechanics 736, 322 (2015)
[14] Dietze G., Rohlfs W., Närich K., Kneer R. & Scheid B., Three-dimensional flow structures in laminar falling liquid films, Journal of Fluid Mechanics 743, 75-123 (2014)
[13] Scheid B., Kalliadasis S., Ruyer-Quil C. & Colinet P., Spontaneous channeling of solitary pulses in heated film flows, Europhysics Letters 84, 64002 (2008)
[12] Scheid B., Kalliadasis S., Ruyer-Quil C. & Colinet P., Interaction of three-dimensional hydrodynamic and thermocapillary instabilities in film flows, Physical Review E 78, 066311 (2008)
[11] Trevelyan P., Scheid B., Kalliadasis S. & Ruyer-Quil C., Heated Falling Films, Journal of Fluid Mechanics 592, 295-334 (2007)
[10] Colinet P., Kaya H., Rossomme S. & Scheid B., Some advances in lubrication-type theories, European Physical Journal Special Topics 146, 377-389 (2007)
[9] Scheid B., Ruyer-Quil C. & Manneville P., Wave Patterns in Film Flows. Modelling and Three-dimensional waves, Journal of Fluid Mechanics 562, 183-222 (2006)
[8] Scheid B., Ruyer-Quil C., Kalliadasis S., Velarde M.G. & Zeytounian R.Kh., Thermocapillary long waves in a liquid film flow. Part 2. linear stability and nonlinear waves, Journal of Fluid Mechanics 538, 223-244 (2005)
[7] Ruyer-Quil C., Scheid B., Kalliadasis S., Velarde M.G. & Zeytounian R.Kh., Thermocapillary long waves in a liquid film flow. Part 1. low dimensional formulation, Journal of Fluid Mechanics 538, 199-222 (2005)
[6] Scheid B., Ruyer-Quil C., Thiele U., Kabov O., Legros J.C. & Colinet P., Validity domain of the Benney equation including Marangoni effect for closed and open flows, Journal of Fluid Mechanics 527, 303-335 (2005)
[5] Skotheim J.M., Thiele U. & Scheid B., On the instability of a falling film due to localized heating, Journal of Fluid Mechanics 475, 1-19 (2003)
[4] Scheid B., Oron A., Colinet P., Thiele U. & Legros J.C., Nonlinear evolution of non-uniformly heated falling liquid films, Physics of Fluids 14, 4130-4151 (2002). Erratum: Phys. Fluids 15, 583 (2003)
[3] Kabov O.A., Scheid B., Sharina I.A. & Legros J.C., Heat transfer and rivulet structures formation in a falling thin liquid film locally heated, International Journal of Thermal Sciences 41, 664-772 (2002)
[2] Miladinova S., Staykova D. Lebon G. & Scheid B., Effect of nonuniform wall heating on the three-dimensional secondary instability of falling films, Acta Mechanica 159, 79-91 (2002)
[1] Kabov O.A., Scheid B., Marchuk I.V. & Legros J.C., Deformation of the free surface in a moving locally-heated thin liquid layer, Fluid Dynamics 36(3), 521-528 (2001)